Lektion VEK01: Einführung zu Vektoren
MatheretterInhalte der Lektion
-
Was ist ein Vektor?
-
Wo kommt der Begriff Vektor her?
-
Was sind die Komponenten des Vektors?
-
Wie werden Vektoren geometrisch und algebraisch definiert?
-
Wie notiert man Vektoren richtig?
-
Welche Anwendungsbeispiele gibt es für Vektoren?
-
Wann sind Vektoren gleich?
- Quelle: https://www.matheretter.de/kurse/vek/einfuhrung
Videos
Video: VEK01-1 Einführung Vektoren - Geometrische Verschiebung berechnen
-
Dies ist die erste Lektion zu den Vektoren. Hier lernen wir, was hinter dem Begriff „Vektor“ steckt, wozu man Vektoren benutzen kann und wie sie uns beim Rechnen helfen.
-
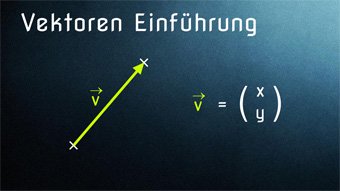
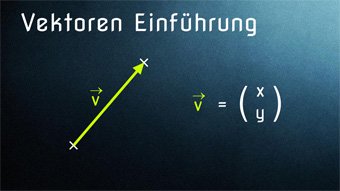
Für Vektoren in der Ebene gibt es mehrere Definitionen. Die geometrische Definition lautet: Ein Vektor ist eine gerichtete Strecke. Die algebraische ("rechnerische") Definition lautet: Ein Vektor ist ein Zahlenpaar. Erfahrt hierzu mehr in den Videos.
-
Was bedeutet Vektor, geometrische Verschiebung in der Ebene mit Vektoren exakt berechnen, Komponenten des Vektors, Vektor als Pfeile mit bestimmter Länge und bestimmter Richtung, Vektornotation, Repräsentanten des Vektors.
Video: VEK01-2 Einführung Vektoren - Definition und Anwendungsbeispiele
-
Was ist ein Vektor? Definition geometrisch und als Zahlenpaar. Schreibweisen für Vektoren. Geschwindigkeit als Anwendungsbeispiele für Vektoren: Gleichförmige Bewegung, kreisförmige Bewegung, Bewegung mit Verzögerung. Übungen zur Gleichheit von Vektoren.
Artikel im Wiki
Wiki: Vektoren - Einführung
Wiki: Vektor-Schreibweise (Spaltenvektor, Zeilenvektor)
Wiki: Besonderheit von Vektoren: Ortsunabhängig
Wiki: Gleichheit von Vektoren
Rechner
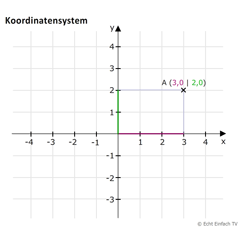
Rechner: Koordinatensystem (Linien 2)
-
In diesem Koordinatensystem bewegt ihr einen Punkt, dessen Koordinaten P(x|y) angezeigt werden. Die Linien helfen euch beim Ablesen.
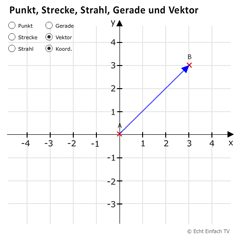
Rechner: Punkt, Strecke, Strahl, Gerade, Vektor
-
Hier könnt ihr euch testen, ob ihr den Unterschied zwischen Punkt, Strecke, Strahl, Gerade und Vektor erkennt.
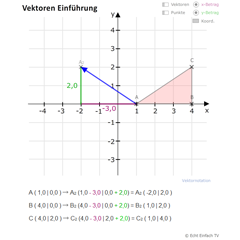
Rechner: Vektoren Einführung
-
Dieses Programm ist eine Einführung in die Vektoren. Eine geometrische Verschiebung wird durch Vektoren (Zahlenpaare) exakt berechenbar gemacht.
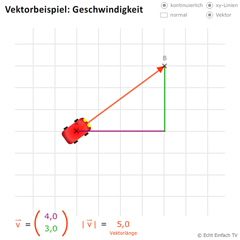
Rechner: Vektorbeispiel Geschwindigkeit 1
-
Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine gleichförmige Bewegung ausführen lassen.
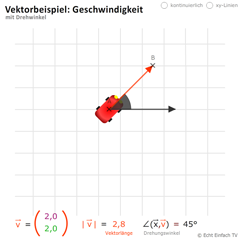
Rechner: Vektorbeispiel Geschwindigkeit 2
-
Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine kreisförmige Bewegung ausführen lassen.
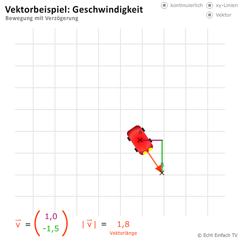
Rechner: Vektorbeispiel Geschwindigkeit 3
-
Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine verzögerte Bewegung ausführen lassen.